#87: Two-color pyrometry with IRt/c's
The IRt/c.L2 Method
For many bare metal temperature monitoring applications, emissivity variations are too extreme for even the IRt/c-LoE models to provide reliable information. A common problem is aluminum, since emissivity is low and variable due to alloying, surface oxidation, surface finish variations, etc.
The traditional non-contact infrared solution has been two-color pyrometry, since this method yields significant improvements over single wavelength devices by ratioing signals at two nearby wavelengths, and thus deducing temperature from the ratio. The major drawbacks of conventional two color systems are size, complexity, and cost. The IRt/c innovation, and the availability of inexpensive computational power, have made possible a simple, reliable substitute for conventional two color pyrometry at a small fraction of the cost and small fraction of the size.
The IRt/c.L2 method of two color pyrometry incorporates the following:
- A short wave (LoE) IRt/c model and long wave IRt/c model viewing the same target area
- Two thermocouple input channels to a computer or PLC
- Computational ability to solve two equations in two unknowns on-line
Depending on the models selected, the cost for such a system can be well under $1000.
The equations to be solved are as follows:
For the short wave (LoE) model:

For the long wave model (example IRt/c.2-K-440F/220C):

where Ssw and Slw are signals produced in millivolts (referenced to 0°C cold junction compensation), e is emissivity, T is target temperature, and A is an arbitrary calibration constant that represents the position of the adjustment screw for the adjustable LoE model.
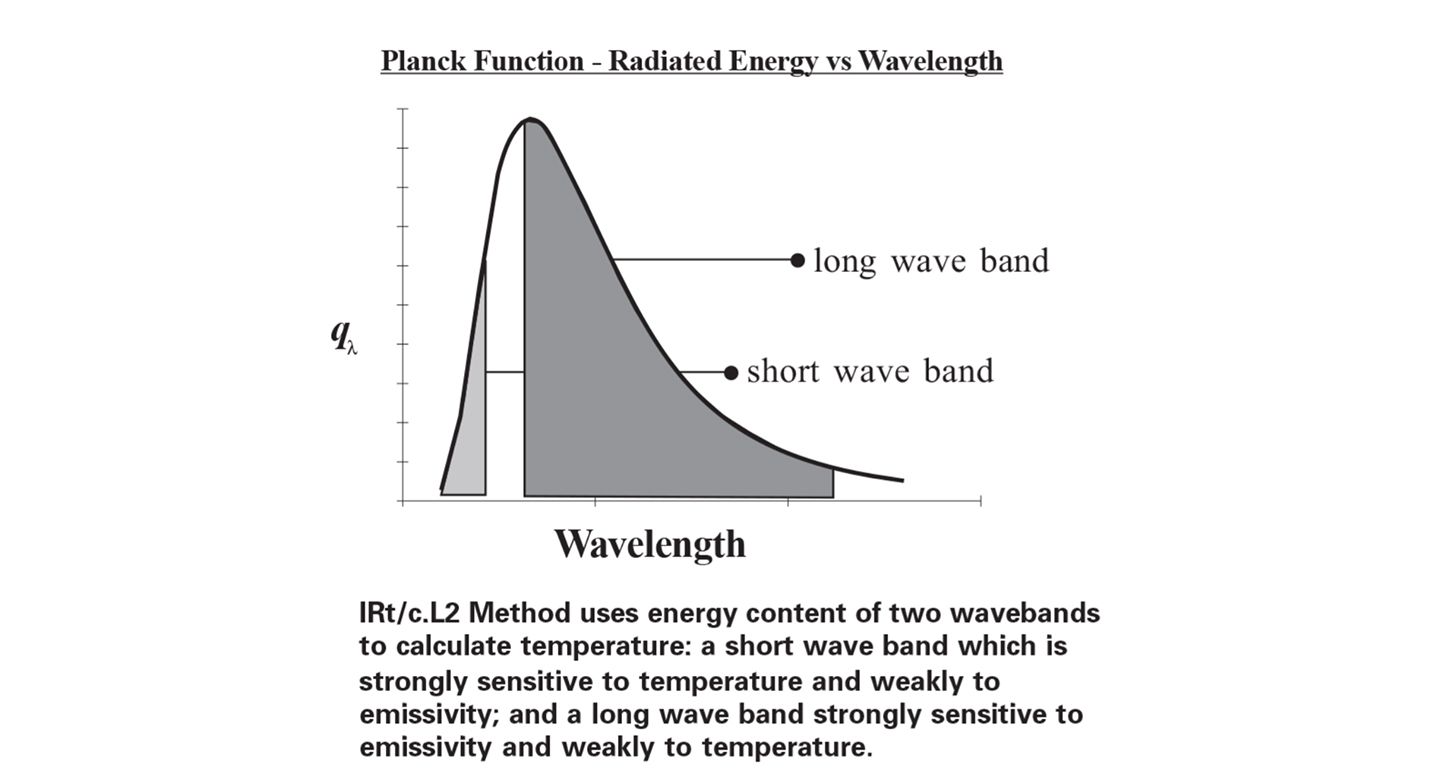
IRt/c.L2 Method uses energy content of two wavebands to calculate temperature: a short wave band which is strongly sensitive to temperature and weakly to emissivity; and a long wave band strongly sensitive to emissivity and weakly to temperature.
An initial calibration has to be performed with both devices viewing the same known target temperature. The value for e is immediately computed by the Slw equation, and the value for A by the Ssw equation. A variety of computational methods can be employed to compute e and T continuously from the two equations in two unknowns, with the simplest being a computation of differentials in signal relative to the initial calibration. The only assumption required for the method to work in its differential form is that the ratio of emissivities for the two wave bands employed remain constant, i.e. (esw / elw) = constant.
For the example and recommended combination of IRt/c.10A-LoE (short wave), and IRt/c.2-K- 440F/220C (long wave) these wavelength bands are 0.1 to 5 micron and 6.5 to 14 micron respectively. Note that the emissivity coefficient can include any effect that is not wavelength dependent, such as intervening dust, partial obstruction, or target smaller than the fields-of-view.